Which is the graph of linear inequality 6x 2y 10 – Delving into the realm of linear inequalities, we embark on a journey to decipher the graph of 6x + 2y ≤ 10. This inequality represents a boundary that divides the coordinate plane into regions, each with its unique properties. Our exploration will unravel the steps involved in graphing this inequality, identifying its solution region, and uncovering its practical applications.

To begin our investigation, we establish the equation of the line 6x + 2y = 10, which forms the boundary of the inequality. By determining its slope and y-intercept, we can plot the line on a coordinate plane. The region below this line, where the inequality holds true, constitutes the solution region.

Graphing Linear Inequalities: Which Is The Graph Of Linear Inequality 6x 2y 10

Linear inequalities are mathematical expressions that compare a linear function to a constant. They are used to represent relationships between variables where one variable is less than or greater than a certain value.

To graph a linear inequality, follow these steps:

• Graph the line represented by the linear equation.
• Determine which side of the line satisfies the inequality.
• Shade the region on that side of the line to represent the solution region.

Identifying the Graph of 6x + 2y ≤ 10, Which is the graph of linear inequality 6x 2y 10

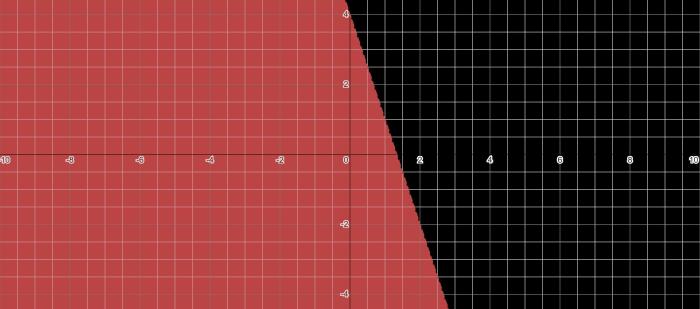
The equation of the line represented by 6x + 2y = 10 is y = -3x + 5.

The slope of the line is -3 and the y-intercept is 5.

Plot the line on a coordinate plane.

To determine which side of the line satisfies the inequality, substitute a point into the inequality.

For example, the point (0, 0) satisfies the inequality because 6(0) + 2(0) = 0 ≤ 10.

Therefore, the solution region is the region below the line.

Analyzing the Solution Region

The solution region for 6x + 2y ≤ 10 is the set of all points that satisfy the inequality.

The solution region is a closed half-plane.

The line 6x + 2y = 10 is the boundary of the solution region.

Points that lie on the boundary of the solution region satisfy the inequality as an equality.

Points that lie inside the solution region satisfy the inequality as a strict inequality.

Points that lie outside the solution region do not satisfy the inequality.

Applications of Linear Inequalities

Linear inequalities have numerous applications in various fields, including:

• Economics: Modeling supply and demand, budgeting, and profit maximization.
• Physics: Describing motion, force, and energy.
• Chemistry: Representing chemical reactions and equilibrium.
• Computer science: Optimizing algorithms and data structures.

Q&A

What is the slope of the line 6x + 2y = 10?

-3

What is the y-intercept of the line 6x + 2y = 10?

5

How do you determine the solution region for the inequality 6x + 2y ≤ 10?

Shade the region below the line 6x + 2y = 10.